Exploring Fully Homomorphic Encryption
2020 Jul 20
See all posts
Exploring Fully Homomorphic Encryption
Special thanks to Karl Floersch and Dankrad Feist for
review
Fully homomorphic encryption has for a long time been considered one
of the holy grails of cryptography. The promise of fully homomorphic
encryption (FHE) is powerful: it is a type of encryption that allows a
third party to perform computations on encrypted data, and get an
encrypted result that they can hand back to whoever has the decryption
key for the original data, without the third party being able
to decrypt the data or the result themselves.

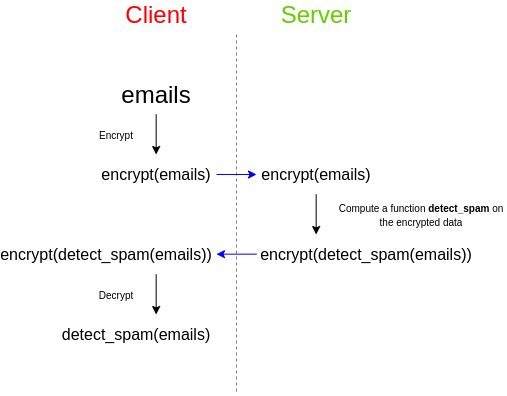
As a simple example, imagine that you have a set of emails, and you
want to use a third party spam filter to check whether or not they are
spam. The spam filter has a desire for privacy of their
algorithm: either the spam filter provider wants to keep their
source code closed, or the spam filter depends on a very large database
that they do not want to reveal publicly as that would make attacking
easier, or both. However, you care about the privacy of your
data, and don't want to upload your unencrypted emails to a third
party. So here's how you do it:
Fully homomorphic encryption has many applications, including in the
blockchain space. One key example is that can be used to implement
privacy-preserving light clients (the light client hands the server an
encrypted index i, the server computes and returns
data[0] * (i = 0) + data[1] * (i = 1) + ... + data[n] * (i = n),
where data[i] is the i'th piece of data in a block or state
along with its Merkle branch and (i = k) is an expression
that returns 1 if i = k and otherwise 0; the light client
gets the data it needs and the server learns nothing about what the
light client asked).
It can also be used for:
- More efficient stealth
address protocols, and more generally scalability solutions to
privacy-preserving protocols that today require each user to personally
scan the entire blockchain for incoming transactions
- Privacy-preserving data-sharing marketplaces that let users allow
some specific computation to be performed on their data while keeping
full control of their data for themselves
- An ingredient in more powerful cryptographic primitives, such as
more efficient multi-party computation protocols and perhaps eventually
obfuscation
And it turns out that fully homomorphic encryption is, conceptually,
not that difficult to understand!
Partially,
Somewhat, Fully homomorphic encryption
First, a note on definitions. There are different kinds of
homomorphic encryption, some more powerful than others, and they are
separated by what kinds of functions one can compute on the encrypted
data.
- Partially homomorphic encryption allows evaluating
only a very limited set of operations on encrypted data: either
just additions (so given
encrypt(a) and
encrypt(b) you can compute encrypt(a+b)), or
just multiplications (given encrypt(a) and
encrypt(b) you can compute encrypt(a*b)).
- Somewhat homomorphic encryption allows computing
additions as well as a limited number of multiplications
(alternatively, polynomials up to a limited degree). That is, if you get
encrypt(x1) ... encrypt(xn) (assuming these are "original"
encryptions and not already the result of homomorphic computation), you
can compute encrypt(p(x1 ... xn)), as long as
p(x1 ... xn) is a polynomial with degree
< D for some specific degree bound D
(D is usually very low, think 5-15).
- Fully homomorphic encryption allows unlimited
additions and multiplications. Additions and multiplications let you
replicate any binary circuit gates (
AND(x, y) = x*y,
OR(x, y) = x+y-x*y, XOR(x, y) = x+y-2*x*y or
just x+y if you only care about even vs odd,
NOT(x) = 1-x...), so this is sufficient to do arbitrary
computation on encrypted data.
Partially homomorphic encryption is fairly easy; eg. RSA has a
multiplicative homomorphism: \(enc(x) =
x^e\), \(enc(y) = y^e\), so
\(enc(x) * enc(y) = (xy)^e = enc(xy)\).
Elliptic curves can offer similar properties with addition. Allowing
both addition and multiplication is, it turns out,
significantly harder.
A simple somewhat-HE
algorithm
Here, we will go through a somewhat-homomorphic encryption algorithm
(ie. one that supports a limited number of multiplications) that is
surprisingly simple. A more complex version of this category of
technique was used by Craig Gentry to create the first-ever
fully homomorphic scheme in 2009. More recent efforts have
switched to using different schemes based on vectors and matrices, but
we will still go through this technique first.
We will describe all of these encryption schemes as
secret-key schemes; that is, the same key is used to encrypt
and decrypt. Any secret-key HE scheme can be turned into a public key
scheme easily: a "public key" is typically just a set of many
encryptions of zero, as well as an encryption of one (and possibly more
powers of two). To encrypt a value, generate it by adding together the
appropriate subset of the non-zero encryptions, and then adding a random
subset of the encryptions of zero to "randomize" the ciphertext and make
it infeasible to tell what it represents.
The secret key here is a large prime, \(p\) (think of \(p\) as having hundreds or even thousands of
digits). The scheme can only encrypt 0 or 1, and "addition" becomes XOR,
ie. 1 + 1 = 0. To encrypt a value \(m\)
(which is either 0 or 1), generate a large random value \(R\) (this will typically be even larger
than \(p\)) and a smaller random value
\(r\) (typically much smaller than
\(p\)), and output:
\[enc(m) = R * p + r * 2 + m\]
To decrypt a ciphertext \(ct\),
compute:
\[dec(ct) = (ct\ mod\ p)\ mod\
2\]
To add two ciphertexts \(ct_1\) and
\(ct_2\), you simply, well, add them:
\(ct_1 + ct_2\). And to multiply two
ciphertexts, you once again... multiply them: \(ct_1 * ct_2\). We can prove the homomorphic
property (that the sum of the encryptions is an encryption of the sum,
and likewise for products) as follows.
Let:
\[ct_1 = R_1 * p + r_1 * 2 + m_1\]
\[ct_2 = R_2 * p + r_2 * 2 + m_2\]
We add:
\[ct_1 + ct_2 = R_1 * p + R_2 * p + r_1 *
2 + r_2 * 2 + m_1 + m_2\]
Which can be rewritten as:
\[(R_1 + R_2) * p + (r_1 + r_2) * 2 + (m_1
+ m_2)\]
Which is of the exact same "form" as a ciphertext of \(m_1 + m_2\). If you decrypt it, the first
\(mod\ p\) removes the first term, the
second \(mod\ 2\) removes the second
term, and what's left is \(m_1 + m_2\)
(remember that if \(m_1 = 1\) and \(m_2 = 1\) then the 2 will get absorbed into
the second term and you'll be left with zero). And so, voila, we have
additive homomorphism!
Now let's check multiplication:
\[ct_1 * ct_2 = (R_1 * p + r_1 * 2 + m_1)
* (R_2 * p + r_2 * 2 + m_2)\]
Or:
\[(R_1 * R_2 * p + r_1 * 2 + m_1 + r_2 * 2
+ m_2) * p + \] \[(r_1 * r_2 * 2 + r_1
* m_2 + r_2 * m_1) * 2 + \] \[(m_1 *
m_2)\]
This was simply a matter of expanding the product above, and grouping
together all the terms that contain \(p\), then all the remaining terms that
contain \(2\), and finally the
remaining term which is the product of the messages. If you decrypt,
then once again the \(mod\ p\) removes
the first group, the \(mod\ 2\) removes
the second group, and only \(m_1 *
m_2\) is left.
But there are two problems here: first, the size of the ciphertext
itself grows (the length roughly doubles when you multiply), and second,
the "noise" (also often called "error") in the smaller \(\* 2\) term also gets quadratically bigger.
Adding this error into the ciphertexts was necessary because the
security of this scheme is based on the approximate
GCD problem:
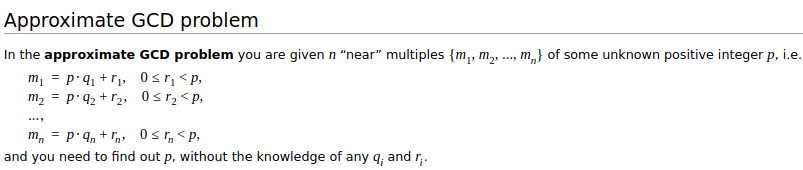
Had we instead used the "exact GCD problem", breaking the system
would be easy: if you just had a set of expressions of the form \(p * R_1 + m_1\), \(p * R_2 + m_2\)..., then you could use the Euclidean
algorithm to efficiently compute the greatest common divisor \(p\). But if the ciphertexts are only
approximate multiples of \(p\)
with some "error", then extracting \(p\) quickly becomes impractical, and so the
scheme can be secure.
Unfortunately, the error introduces the inherent limitation that if
you multiply the ciphertexts by each other enough times, the error
eventually grows big enough that it exceeds \(p\), and at that point the \(mod\ p\) and \(mod\ 2\) steps "interfere" with each other,
making the data unextractable. This will be an inherent tradeoff in all
of these homomorphic encryption schemes: extracting information from
approximate equations "with errors" is much harder than
extracting information from exact equations, but any error you add
quickly increases as you do computations on encrypted data, bounding the
amount of computation that you can do before the error becomes
overwhelming. And this is why these schemes are only "somewhat"
homomorphic.
Bootstrapping
There are two classes of solution to this problem. First, in many
somewhat homomorphic encryption schemes, there are clever tricks to make
multiplication only increase the error by a constant factor (eg. 1000x)
instead of squaring it. Increasing the error by 1000x still sounds by a
lot, but keep in mind that if \(p\) (or
its equivalent in other schemes) is a 300-digit number, that means that
you can multiply numbers by each other 100 times, which is enough to
compute a very wide class of computations. Second, there is Craig
Gentry's technique of "bootstrapping".
Suppose that you have a ciphertext \(ct\) that is an encryption of some \(m\) under a key \(p\), that has a lot of error. The idea is
that we "refresh" the ciphertext by turning it into a new ciphertext of
\(m\) under another key \(p_2\), where this process "clears out" the
old error (though it will introduce a fixed amount of new error). The
trick is quite clever. The holder of \(p\) and \(p_2\) provides a "bootstrapping key" that
consists of an encryption of the bits of \(p\) under the key \(p_2\), as well as the public key for \(p_2\). Whoever is doing computations on
data encrypted under \(p\) would then
take the bits of the ciphertext \(ct\),
and individually encrypt these bits under \(p_2\). They would then homomorphically
compute the decryption under \(p\)
using these ciphertexts, and get out the single bit, which would be
\(m\) encrypted under \(p_2\).
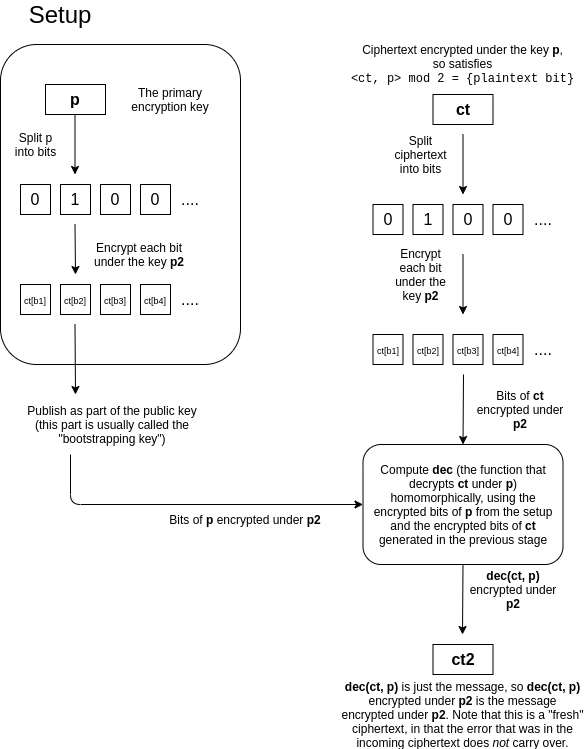
This is difficult to understand, so we can restate it as follows. The
decryption procedure \(dec(ct, p)\)
is itself a computation, and so it can itself be
implemented as a circuit that takes as input the bits of \(ct\) and the bits of \(p\), and outputs the decrypted bit \(m \in {0, 1}\). If someone has a ciphertext
\(ct\) encrypted under \(p\), a public key for \(p_2\), and the bits of \(p\) encrypted under \(p_2\), then they can compute \(dec(ct, p) = m\) "homomorphically", and get
out \(m\) encrypted under \(p_2\). Notice that the decryption procedure
itself washes away the old error; it just outputs 0 or 1. The decryption
procedure is itself a circuit, which contains additions or
multiplications, so it will introduce new error, but this new error
does not depend on the amount of error in the original
encryption.
(Note that we can avoid having a distinct new key \(p_2\) (and if you want to bootstrap
multiple times, also a \(p_3\), \(p_4\)...) by just setting \(p_2 = p\). However, this introduces a new
assumption, usually called "circular security"; it becomes
more difficult to formally prove security if you do this, though
many cryptographers think it's fine and circular security poses no
significant risk in practice)
But.... there is a catch. In the scheme as described above (using
circular security or not), the error blows up so quickly that even the
decryption circuit of the scheme itself is too much for it. That is, the
new \(m\) encrypted under \(p_2\) would already have so much
error that it is unreadable. This is because each AND gate doubles the
bit-length of the error, so a scheme using a \(d\)-bit modulus \(p\) can only handle less than \(log(d)\) multiplications (in series), but
decryption requires computing \(mod\
p\) in a circuit made up of these binary logic gates, which
requires... more than \(log(d)\)
multiplications.
Craig Gentry came up with clever techniques to get around this
problem, but they are arguably too complicated to explain; instead, we
will skip straight to newer work from 2011 and 2013, that solves this
problem in a different way.
Learning with errors
To move further, we will introduce a different type of
somewhat-homomorphic encryption introduced by Brakerski and
Vaikuntanathan in 2011, and show how to bootstrap it. Here, we will move
away from keys and ciphertexts being integers, and instead have
keys and ciphertexts be vectors. Given a key \(k = {k_1, k_2 .... k_n}\), to encrypt a
message \(m\), construct a vector \(c = {c_1, c_2 ... c_n}\) such that the
inner product (or "dot product") \(<c, k> = c_1k_1 + c_2k_1 + ... +
c_nk_n\), modulo some fixed number \(p\), equals \(m+2e\) where \(m\) is the message (which must be 0 or 1),
and \(e\) is a small (much smaller than
\(p\)) "error" term. A "public key"
that allows encryption but not decryption can be constructed, as before,
by making a set of encryptions of 0; an encryptor can randomly combine a
subset of these equations and add 1 if the message they are encrypting
is 1. To decrypt a ciphertext \(c\)
knowing the key \(k\), you would
compute \(<c, k>\) modulo \(p\), and see if the result is odd or even
(this is the same "mod p mod 2" trick we used earlier). Note that here
the \(mod\ p\) is typically a
"symmetric" mod, that is, it returns a number between \(-\frac{p}{2}\) and \(\frac{p}{2}\) (eg. 137 mod 10 = -3, 212 mod
10 = 2); this allows our error to be positive or negative. Additionally,
\(p\) does not necessarily have to be
prime, though it does need to be odd.
|
Key
|
3
|
14
|
15
|
92
|
65
|
|
Ciphertext
|
2
|
71
|
82
|
81
|
8
|
The key and the ciphertext are both vectors, in this example
of five elements each.
In this example, we set the modulus \(p =
103\). The dot product is
3 * 2 + 14 * 71 + 15 * 82 + 92 * 81 + 65 * 8 = 10202, and
\(10202 = 99 * 103 + 5\). 5 itself is
of course \(2 * 2 + 1\), so the message
is 1. Note that in practice, the first element of the key is often set
to \(1\); this makes it easier to
generate ciphertexts for a particular value (see if you can figure out
why).
The security of the scheme is based on an assumption known as "learning with
errors" (LWE) - or, in more jargony but also more understandable
terms, the hardness of solving systems of equations with
errors.

A ciphertext can itself be viewed as an equation: \(k_1c_1 + .... + k_nc_n \approx 0\), where
the key \(k_1 ... k_n\) is the
unknowns, the ciphertext \(c_1 ...
c_n\) is the coefficients, and the equality is only approximate
because of both the message (0 or 1) and the error (\(2e\) for some relatively small \(e\)). The LWE assumption ensures that even
if you have access to many of these ciphertexts, you cannot recover
\(k\).
Note that in some descriptions of LWE, <c, k> can
equal any value, but this value must be provided as part of the
ciphertext. This is mathematically equivalent to the <c, k> = m+2e
formulation, because you can just add this answer to the end of the
ciphertext and add -1 to the end of the key, and get two vectors that
when multiplied together just give m+2e. We'll use the formulation that
requires <c, k> to be near-zero (ie. just m+2e) because it is
simpler to work with.
Multiplying ciphertexts
It is easy to verify that the encryption is additive: if \(<ct_1, k> = 2e_1 + m_1\) and \(<ct_2, k> = 2e_2 + m_2\), then \(<ct_1 + ct_2, k> = 2(e_1 + e_2) + m_1 +
m_2\) (the addition here is modulo \(p\)). What is harder is multiplication:
unlike with numbers, there is no natural way to multiply two length-n
vectors into another length-n vector. The best that we can do is the outer product: a
vector containing the products of each possible pair where the first
element comes from the first vector and the second element comes from
the second vector. That is, \(a \otimes b =
a_1b_1 + a_2b_1 + ... + a_nb_1 + a_1b_2 + ... + a_nb_2 + ... +
a_nb_n\). We can "multiply ciphertexts" using the convenient
mathematical identity \(<a \otimes b, c
\otimes d> = <a, c> * <b, d>\).
Given two ciphertexts \(c_1\) and
\(c_2\), we compute the outer product
\(c_1 \otimes c_2\). If both \(c_1\) and \(c_2\) were encrypted with \(k\), then \(<c_1, k> = 2e_1 + m_1\) and \(<c_2, k> = 2e_2 + m_2\). The outer
product \(c_1 \otimes c_2\) can be
viewed as an encryption of \(m_1 *
m_2\) under \(k \otimes k\); we
can see this by looking what happens when we try to decrypt with \(k \otimes k\):
\[<c_1 \otimes c_2, k \otimes
k>\] \[= <c_1, k> * <c_2,
k>\] \[ = (2e_1 + m_1) * (2e_2 +
m_2)\] \[ = 2(e_1m_2 + e_2m_1 +
2e_1e_2) + m_1m_2\]
So this outer-product approach works. But there is, as you may have
already noticed, a catch: the size of the ciphertext, and the key, grows
quadratically.
Relinearization
We solve this with a relinearization procedure. The
holder of the private key \(k\)
provides, as part of the public key, a "relinearization key", which you
can think of as "noisy" encryptions of \(k
\otimes k\) under \(k\). The
idea is that we provide these encrypted pieces of \(k \otimes k\) to anyone performing the
computations, allowing them to compute the equation \(<c_1 \otimes c_2, k \otimes k>\) to
"decrypt" the ciphertext, but only in such a way that the output comes
back encrypted under \(k\).
It's important to understand what we mean here by "noisy
encryptions". Normally, this encryption scheme only allows encrypting
\(m \in \{0,1\}\), and an "encryption
of \(m\)" is a vector \(c\) such that \(<c, k> = m+2e\) for some small error
\(e\). Here, we're "encrypting"
arbitrary \(m \in \{0,1, 2....p-1\}\).
Note that the error means that you can't fully recover \(m\) from \(c\); your answer will be off by some
multiple of 2. However, it turns out that, for this specific use case,
this is fine.
The relinearization key consists of a set of vectors which, when
inner-producted (modulo \(p\)) with the
key \(k\), give values of the form
\(k_i * k_j * 2^d + 2e\) (mod \(p\)), one such vector for every possible
triple \((i, j, d)\), where \(i\) and \(j\) are indices in the key and \(d\) is an exponent where \(2^d < p\) (note: if the key has length
\(n\), there would be \(n^2 * log(p)\) values in the
relinearization key; make sure you understand why before
continuing).

Example assuming p = 15 and k has length 2. Formally, enc(x)
here means "outputs x+2e if inner-producted with k".
Now, let us take a step back and look again at our goal. We have a
ciphertext which, if decrypted with \(k
\otimes k\), gives \(m_1 *
m_2\). We want a ciphertext which, if decrypted with
\(k\), gives \(m_1 * m_2\). We can do this with the
relinearization key. Notice that the decryption equation \(<ct_1 \otimes ct_2, k \otimes k>\) is
just a big sum of terms of the form \((ct_{1_i} * ct_{2_j}) * k_p * k_q\).
And what do we have in our relinearization key? A bunch of elements
of the form \(2^d * k_p * k_q\),
noisy-encrypted under \(k\), for every
possible combination of \(p\) and \(q\)! Having all the powers of two in our
relinearization key allows us to generate any \((ct_{1_i} * ct_{2_j}) * k_p * k_q\) by just
adding up \(\le log(p)\) powers of two
(eg. 13 = 8 + 4 + 1) together for each \((p,
q)\) pair.
For example, if \(ct_1 = [1, 2]\)
and \(ct_2 = [3, 4]\), then \(ct_1 \otimes ct_2 = [3, 4, 6, 8]\), and
\(enc(<ct_1 \otimes ct_2, k \otimes k>)
= enc(3k_1k_1 + 4k_1k_2 + 6k_2k_1 + 8k_2k_2)\) could be computed
via:
\[enc(k_1 * k_1) + enc(k_1 * k_1 * 2) +
enc(k_1 * k_2 * 4) + \]
\[enc(k_2 * k_1 * 2) + enc(k_2 * k_1 *
4) + enc(k_2 * k_2 * 8) \]
Note that each noisy-encryption in the relinearization key has some
even error \(2e\), and the equation
\(<ct_1 \otimes ct_2, k \otimes
k>\) itself has some error: if \(<ct_1, k> = 2e_1 + m_1\) and \(<ct_2 + k> = 2e_2 + m_2\), then \(<ct_1 \otimes ct_2, k \otimes k> =\)
\(<ct_1, k> * <ct_2 + k>
=\) \(2(2e_1e_2 + e_1m_2 + e_2m_1) +
m_1m_2\). But this total error is still (relatively) small (\(2e_1e_2 + e_1m_2 + e_2m_1\) plus \(n^2 * log(p)\) fixed-size errors from the
realinearization key), and the error is even, and so the result of this
calculation still gives a value which, when inner-producted with \(k\), gives \(m_1
* m_2 + 2e'\) for some "combined error" \(e'\).
The broader technique we used here is a common trick in homomorphic
encryption: provide pieces of the key encrypted under the key itself (or
a different key if you are pedantic about avoiding circular security
assumptions), such that someone computing on the data can compute the
decryption equation, but only in such a way that the output itself is
still encrypted. It was used in bootstrapping above, and it's used here;
it's best to make sure you mentally understand what's going on in both
cases.
This new ciphertext has considerably more error in it: the \(n^2 * log(p)\) different errors from the
portions of the relinearization key that we used, plus the \(2(2e_1e_2 + e_1m_2 + e_2m_1)\) from the
original outer-product ciphertext. Hence, the new ciphertext still does
have quadratically larger error than the original ciphertexts, and so we
still haven't solved the problem that the error blows up too quickly. To
solve this, we move on to another trick...
Modulus switching
Here, we need to understand an important algebraic fact. A ciphertext
is a vector \(ct\), such that \(<ct, k> = m+2e\), where \(m \in \{0,1\}\). But we can also look at
the ciphertext from a different "perspective": consider \(\frac{ct}{2}\) (modulo \(p\)). \(<\frac{ct}{2}, k> = \frac{m}{2} +
e\), where \(\frac{m}{2} \in
\{0,\frac{p+1}{2}\}\). Note that because (modulo \(p\)) \((\frac{p+1}{2})*2 = p+1 = 1\), division by
2 (modulo \(p\)) maps \(1\) to \(\frac{p+1}{2}\); this is a very convenient
fact for us.
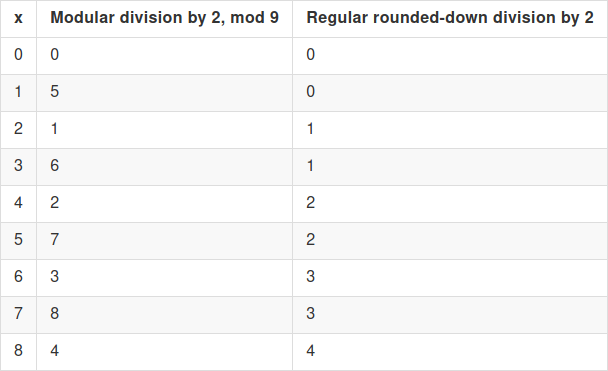
The scheme in this section uses both modular division (ie.
multiplying by the modular
multiplicative inverse) and regular "rounded down" integer division;
make sure you understand how both work and how they are different from
each other.
That is, the operation of dividing by 2 (modulo \(p\)) converts small even numbers into small
numbers, and it converts 1 into \(\frac{p}{2}\) (rounded up). So if we look
at \(\frac{ct}{2}\) (modulo \(p\)) instead of \(ct\), decryption involves computing \(<\frac{ct}{2}, k>\) and seeing if
it's closer to \(0\) or \(\frac{p}{2}\). This "perspective" is much
more robust to certain kinds of errors, where you know the error is
small but can't guarantee that it's a multiple of 2.
Now, here is something we can do to a ciphertext.
- Start: \(<ct, k> = \{0\ or\ 1\} +
2e\ (mod\ p)\)
- Divide \(ct\) by 2 (modulo \(p\)): \(<ct', k> = \{0\ or\ \frac{p}{2}\} + e\
(mod\ p)\)
- Multiply \(ct'\) by \(\frac{q}{p}\) using "regular
rounded-down integer division": \(<ct'', k> = \{0\ or\ \frac{q}{2}\} +
e' + e_2\ (mod\ q)\)
- Multiply \(ct''\) by 2
(modulo \(q\)): \(<ct''', k> = \{0\ or\ 1\} +
2e' + 2e_2\ (mod\ q)\)
Step 3 is the crucial one: it converts a ciphertext under modulus
\(p\) into a ciphertext under modulus
\(q\). The process just involves
"scaling down" each element of \(ct'\) by multiplying by \(\frac{q}{p}\) and rounding down, eg. \(floor(56 * \frac{15}{103}) = floor(8.15533..) =
8\).
The idea is this: if \(<ct', k> =
m*\frac{p}{2} + e\ (mod\ p)\), then we can interpret this as
\(<ct', k> = p(z + \frac{m}{2}) +
e\) for some integer \(z\).
Therefore, \(<ct' * \frac{q}{p}, k>
= q(z + \frac{m}{2}) + e*\frac{p}{q}\). Rounding adds error, but
only a little bit (specifically, up to the size of the values in \(k\), and we can make the values in \(k\) small without sacrificing security).
Therefore, we can say \(<ct' *
\frac{q}{p}, k> = m*\frac{q}{2} + e' + e_2\ (mod\ q)\),
where \(e' = e * \frac{q}{p}\), and
\(e_2\) is a small error from
rounding.
What have we accomplished? We turned a ciphertext with modulus \(p\) and error \(2e\) into a ciphertext with modulus \(q\) and error \(2(floor(e*\frac{p}{q}) + e_2)\), where the
new error is smaller than the original error.
Let's go through the above with an example. Suppose:
- \(ct\) is just one value, \([5612]\)
- \(k = [9]\)
- \(p = 9999\) and \(q = 113\)
\(<ct, k> = 5612 * 9 = 50508 = 9999 *
5 + 2 * 256 + 1\), so \(ct\)
represents the bit 1, but the error is fairly large (\(e = 256\)).
Step 2: \(ct' = \frac{ct}{2} =
2806\) (remember this is modular division; if \(ct\) were instead \(5613\), then we would have \(\frac{ct}{2} = 7806\)). Checking: \(<ct', k> = 2806 * 9 = 25254 = 9999 * 2.5
+ 256.5\)
Step 3: \(ct'' = floor(2806 *
\frac{113}{9999}) = floor(31.7109...) = 31\). Checking: \(<ct'', k> = 279 = 113 * 2.5 -
3.5\)
Step 4: \(ct''' = 31 * 2 =
62\). Checking: \(<ct''', k> = 558 = 113 * 5 - 2 *
4 + 1\)
And so the bit \(1\) is preserved
through the transformation. The crazy thing about this procedure is:
none of it requires knowing \(k\). Now, an astute reader might
notice: you reduced the absolute size of the error (from 256 to
2), but the relative size of the error remained unchanged, and
even slightly increased: \(\frac{256}{9999}
\approx 2.5\%\) but \(\frac{4}{113}
\approx 3.5\%\). Given that it's the relative error that causes
ciphertexts to break, what have we gained here?
The answer comes from what happens to error when you multiply
ciphertexts. Suppose that we start with a ciphertext \(x\) with error 100, and modulus \(p = 10^{16} - 1\). We want to repeatedly
square \(x\), to compute \((((x^2)^2)^2)^2 = x^{16}\). First, the
"normal way":
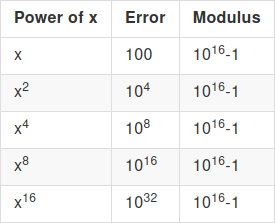
The error blows up too quickly for the computation to be possible.
Now, let's do a modulus reduction after every multiplication. We assume
the modulus reduction is imperfect and increases error by a factor of
10, so a 1000x modulo reduction only reduces error from 10000 to 100
(and not to 10):
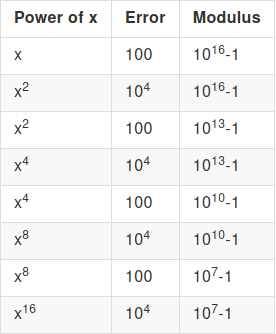
The key mathematical idea here is that the factor by which
error increases in a multiplication depends on the absolute size of the
error, and not its relative size, and so if we keep doing modulus
reductions to keep the error small, each multiplication only increases
the error by a constant factor. And so, with a \(d\) bit modulus (and hence \(\approx 2^d\) room for "error"), we can do
\(O(d)\) multiplications! This is
enough to bootstrap.
Another technique: matrices
Another technique (see Gentry, Sahai, Waters
(2013)) for fully homomorphic encryption involves matrices: instead
of representing a ciphertext as \(ct\)
where \(<ct, k> = 2e + m\), a
ciphertext is a matrix, where \(k * CT = k * m
+ e\) (\(k\), the key, is still
a vector). The idea here is that \(k\)
is a "secret near-eigenvector" - a secret vector which, if you multiply
the matrix by it, returns something very close to either zero or the key
itself.
The fact that addition works is easy: if \(k * CT_1 = m_1 * k + e_1\) and \(k * CT_2 = m_2 * k + e_2\), then \(k * (CT_1 + CT_2) = (m_1 + m_2) * k + (e_1 +
e_2)\). The fact that multiplication works is also easy:
\(k * CT_1 * CT_2\) \(= (m_1 * k + e_1) * CT_2\) \(= m_1 * k * CT_2 + e_1 * CT_2\) \(= m_1 * m_2 * k + m_1 * e_2 + e_1 *
CT_2\)
The first term is the "intended term"; the latter two terms are the
"error". That said, notice that here error does blow up quadratically
(see the \(e_1 * CT_2\) term; the size
of the error increases by the size of each ciphertext element, and the
ciphertext elements also square in size), and you do need some clever
tricks for avoiding this. Basically, this involves turning ciphertexts
into matrices containing their constituent bits before multiplying, to
avoid multiplying by anything higher than 1; if you want to see how this
works in detail I recommend looking at my code: https://github.com/vbuterin/research/blob/master/matrix_fhe/matrix_fhe.py#L121
In addition, the code there, and also https://github.com/vbuterin/research/blob/master/tensor_fhe/homomorphic_encryption.py#L186,
provides simple examples of useful circuits that you can build out of
these binary logical operations; the main example is for adding numbers
that are represented as multiple bits, but one can also make circuits
for comparison (\(<\), \(>\), \(=\)), multiplication, division, and many
other operations.
Since 2012-13, when these algorithms were created, there have been
many optimizations, but they all work on top of these basic frameworks.
Often, polynomials are used instead of integers; this is called ring
LWE. The major challenge is still efficiency: an operation involving
a single bit involves multiplying entire matrices or performing an
entire relinearization computation, a very high overhead. There are
tricks that allow you to perform many bit operations in a single
ciphertext operation, and this is actively being worked on and
improved.
We are quickly getting to the point where many of the applications of
homomorphic encryption in privacy-preserving computation are starting to
become practical. Additionally, research in the more advanced
applications of the lattice-based cryptography used in homomorphic
encryption is rapidly progressing. So this is a space where some things
can already be done today, but we can hopefully look forward to much
more becoming possible over the next decade.
Exploring Fully Homomorphic Encryption
2020 Jul 20 See all postsSpecial thanks to Karl Floersch and Dankrad Feist for review
Fully homomorphic encryption has for a long time been considered one of the holy grails of cryptography. The promise of fully homomorphic encryption (FHE) is powerful: it is a type of encryption that allows a third party to perform computations on encrypted data, and get an encrypted result that they can hand back to whoever has the decryption key for the original data, without the third party being able to decrypt the data or the result themselves.
As a simple example, imagine that you have a set of emails, and you want to use a third party spam filter to check whether or not they are spam. The spam filter has a desire for privacy of their algorithm: either the spam filter provider wants to keep their source code closed, or the spam filter depends on a very large database that they do not want to reveal publicly as that would make attacking easier, or both. However, you care about the privacy of your data, and don't want to upload your unencrypted emails to a third party. So here's how you do it:
Fully homomorphic encryption has many applications, including in the blockchain space. One key example is that can be used to implement privacy-preserving light clients (the light client hands the server an encrypted index
i, the server computes and returnsdata[0] * (i = 0) + data[1] * (i = 1) + ... + data[n] * (i = n), wheredata[i]is the i'th piece of data in a block or state along with its Merkle branch and(i = k)is an expression that returns 1 ifi = kand otherwise 0; the light client gets the data it needs and the server learns nothing about what the light client asked).It can also be used for:
And it turns out that fully homomorphic encryption is, conceptually, not that difficult to understand!
Partially, Somewhat, Fully homomorphic encryption
First, a note on definitions. There are different kinds of homomorphic encryption, some more powerful than others, and they are separated by what kinds of functions one can compute on the encrypted data.
encrypt(a)andencrypt(b)you can computeencrypt(a+b)), or just multiplications (givenencrypt(a)andencrypt(b)you can computeencrypt(a*b)).encrypt(x1) ... encrypt(xn)(assuming these are "original" encryptions and not already the result of homomorphic computation), you can computeencrypt(p(x1 ... xn)), as long asp(x1 ... xn)is a polynomial with degree< Dfor some specific degree boundD(Dis usually very low, think 5-15).AND(x, y) = x*y,OR(x, y) = x+y-x*y,XOR(x, y) = x+y-2*x*yor justx+yif you only care about even vs odd,NOT(x) = 1-x...), so this is sufficient to do arbitrary computation on encrypted data.Partially homomorphic encryption is fairly easy; eg. RSA has a multiplicative homomorphism: \(enc(x) = x^e\), \(enc(y) = y^e\), so \(enc(x) * enc(y) = (xy)^e = enc(xy)\). Elliptic curves can offer similar properties with addition. Allowing both addition and multiplication is, it turns out, significantly harder.
A simple somewhat-HE algorithm
Here, we will go through a somewhat-homomorphic encryption algorithm (ie. one that supports a limited number of multiplications) that is surprisingly simple. A more complex version of this category of technique was used by Craig Gentry to create the first-ever fully homomorphic scheme in 2009. More recent efforts have switched to using different schemes based on vectors and matrices, but we will still go through this technique first.
We will describe all of these encryption schemes as secret-key schemes; that is, the same key is used to encrypt and decrypt. Any secret-key HE scheme can be turned into a public key scheme easily: a "public key" is typically just a set of many encryptions of zero, as well as an encryption of one (and possibly more powers of two). To encrypt a value, generate it by adding together the appropriate subset of the non-zero encryptions, and then adding a random subset of the encryptions of zero to "randomize" the ciphertext and make it infeasible to tell what it represents.
The secret key here is a large prime, \(p\) (think of \(p\) as having hundreds or even thousands of digits). The scheme can only encrypt 0 or 1, and "addition" becomes XOR, ie. 1 + 1 = 0. To encrypt a value \(m\) (which is either 0 or 1), generate a large random value \(R\) (this will typically be even larger than \(p\)) and a smaller random value \(r\) (typically much smaller than \(p\)), and output:
\[enc(m) = R * p + r * 2 + m\]
To decrypt a ciphertext \(ct\), compute:
\[dec(ct) = (ct\ mod\ p)\ mod\ 2\]
To add two ciphertexts \(ct_1\) and \(ct_2\), you simply, well, add them: \(ct_1 + ct_2\). And to multiply two ciphertexts, you once again... multiply them: \(ct_1 * ct_2\). We can prove the homomorphic property (that the sum of the encryptions is an encryption of the sum, and likewise for products) as follows.
Let:
\[ct_1 = R_1 * p + r_1 * 2 + m_1\] \[ct_2 = R_2 * p + r_2 * 2 + m_2\]
We add:
\[ct_1 + ct_2 = R_1 * p + R_2 * p + r_1 * 2 + r_2 * 2 + m_1 + m_2\]
Which can be rewritten as:
\[(R_1 + R_2) * p + (r_1 + r_2) * 2 + (m_1 + m_2)\]
Which is of the exact same "form" as a ciphertext of \(m_1 + m_2\). If you decrypt it, the first \(mod\ p\) removes the first term, the second \(mod\ 2\) removes the second term, and what's left is \(m_1 + m_2\) (remember that if \(m_1 = 1\) and \(m_2 = 1\) then the 2 will get absorbed into the second term and you'll be left with zero). And so, voila, we have additive homomorphism!
Now let's check multiplication:
\[ct_1 * ct_2 = (R_1 * p + r_1 * 2 + m_1) * (R_2 * p + r_2 * 2 + m_2)\]
Or:
\[(R_1 * R_2 * p + r_1 * 2 + m_1 + r_2 * 2 + m_2) * p + \] \[(r_1 * r_2 * 2 + r_1 * m_2 + r_2 * m_1) * 2 + \] \[(m_1 * m_2)\]
This was simply a matter of expanding the product above, and grouping together all the terms that contain \(p\), then all the remaining terms that contain \(2\), and finally the remaining term which is the product of the messages. If you decrypt, then once again the \(mod\ p\) removes the first group, the \(mod\ 2\) removes the second group, and only \(m_1 * m_2\) is left.
But there are two problems here: first, the size of the ciphertext itself grows (the length roughly doubles when you multiply), and second, the "noise" (also often called "error") in the smaller \(\* 2\) term also gets quadratically bigger. Adding this error into the ciphertexts was necessary because the security of this scheme is based on the approximate GCD problem:
Had we instead used the "exact GCD problem", breaking the system would be easy: if you just had a set of expressions of the form \(p * R_1 + m_1\), \(p * R_2 + m_2\)..., then you could use the Euclidean algorithm to efficiently compute the greatest common divisor \(p\). But if the ciphertexts are only approximate multiples of \(p\) with some "error", then extracting \(p\) quickly becomes impractical, and so the scheme can be secure.
Unfortunately, the error introduces the inherent limitation that if you multiply the ciphertexts by each other enough times, the error eventually grows big enough that it exceeds \(p\), and at that point the \(mod\ p\) and \(mod\ 2\) steps "interfere" with each other, making the data unextractable. This will be an inherent tradeoff in all of these homomorphic encryption schemes: extracting information from approximate equations "with errors" is much harder than extracting information from exact equations, but any error you add quickly increases as you do computations on encrypted data, bounding the amount of computation that you can do before the error becomes overwhelming. And this is why these schemes are only "somewhat" homomorphic.
Bootstrapping
There are two classes of solution to this problem. First, in many somewhat homomorphic encryption schemes, there are clever tricks to make multiplication only increase the error by a constant factor (eg. 1000x) instead of squaring it. Increasing the error by 1000x still sounds by a lot, but keep in mind that if \(p\) (or its equivalent in other schemes) is a 300-digit number, that means that you can multiply numbers by each other 100 times, which is enough to compute a very wide class of computations. Second, there is Craig Gentry's technique of "bootstrapping".
Suppose that you have a ciphertext \(ct\) that is an encryption of some \(m\) under a key \(p\), that has a lot of error. The idea is that we "refresh" the ciphertext by turning it into a new ciphertext of \(m\) under another key \(p_2\), where this process "clears out" the old error (though it will introduce a fixed amount of new error). The trick is quite clever. The holder of \(p\) and \(p_2\) provides a "bootstrapping key" that consists of an encryption of the bits of \(p\) under the key \(p_2\), as well as the public key for \(p_2\). Whoever is doing computations on data encrypted under \(p\) would then take the bits of the ciphertext \(ct\), and individually encrypt these bits under \(p_2\). They would then homomorphically compute the decryption under \(p\) using these ciphertexts, and get out the single bit, which would be \(m\) encrypted under \(p_2\).
This is difficult to understand, so we can restate it as follows. The decryption procedure \(dec(ct, p)\) is itself a computation, and so it can itself be implemented as a circuit that takes as input the bits of \(ct\) and the bits of \(p\), and outputs the decrypted bit \(m \in {0, 1}\). If someone has a ciphertext \(ct\) encrypted under \(p\), a public key for \(p_2\), and the bits of \(p\) encrypted under \(p_2\), then they can compute \(dec(ct, p) = m\) "homomorphically", and get out \(m\) encrypted under \(p_2\). Notice that the decryption procedure itself washes away the old error; it just outputs 0 or 1. The decryption procedure is itself a circuit, which contains additions or multiplications, so it will introduce new error, but this new error does not depend on the amount of error in the original encryption.
(Note that we can avoid having a distinct new key \(p_2\) (and if you want to bootstrap multiple times, also a \(p_3\), \(p_4\)...) by just setting \(p_2 = p\). However, this introduces a new assumption, usually called "circular security"; it becomes more difficult to formally prove security if you do this, though many cryptographers think it's fine and circular security poses no significant risk in practice)
But.... there is a catch. In the scheme as described above (using circular security or not), the error blows up so quickly that even the decryption circuit of the scheme itself is too much for it. That is, the new \(m\) encrypted under \(p_2\) would already have so much error that it is unreadable. This is because each AND gate doubles the bit-length of the error, so a scheme using a \(d\)-bit modulus \(p\) can only handle less than \(log(d)\) multiplications (in series), but decryption requires computing \(mod\ p\) in a circuit made up of these binary logic gates, which requires... more than \(log(d)\) multiplications.
Craig Gentry came up with clever techniques to get around this problem, but they are arguably too complicated to explain; instead, we will skip straight to newer work from 2011 and 2013, that solves this problem in a different way.
Learning with errors
To move further, we will introduce a different type of somewhat-homomorphic encryption introduced by Brakerski and Vaikuntanathan in 2011, and show how to bootstrap it. Here, we will move away from keys and ciphertexts being integers, and instead have keys and ciphertexts be vectors. Given a key \(k = {k_1, k_2 .... k_n}\), to encrypt a message \(m\), construct a vector \(c = {c_1, c_2 ... c_n}\) such that the inner product (or "dot product") \(<c, k> = c_1k_1 + c_2k_1 + ... + c_nk_n\), modulo some fixed number \(p\), equals \(m+2e\) where \(m\) is the message (which must be 0 or 1), and \(e\) is a small (much smaller than \(p\)) "error" term. A "public key" that allows encryption but not decryption can be constructed, as before, by making a set of encryptions of 0; an encryptor can randomly combine a subset of these equations and add 1 if the message they are encrypting is 1. To decrypt a ciphertext \(c\) knowing the key \(k\), you would compute \(<c, k>\) modulo \(p\), and see if the result is odd or even (this is the same "mod p mod 2" trick we used earlier). Note that here the \(mod\ p\) is typically a "symmetric" mod, that is, it returns a number between \(-\frac{p}{2}\) and \(\frac{p}{2}\) (eg. 137 mod 10 = -3, 212 mod 10 = 2); this allows our error to be positive or negative. Additionally, \(p\) does not necessarily have to be prime, though it does need to be odd.
In this example, we set the modulus \(p = 103\). The dot product is
3 * 2 + 14 * 71 + 15 * 82 + 92 * 81 + 65 * 8 = 10202, and \(10202 = 99 * 103 + 5\). 5 itself is of course \(2 * 2 + 1\), so the message is 1. Note that in practice, the first element of the key is often set to \(1\); this makes it easier to generate ciphertexts for a particular value (see if you can figure out why).The security of the scheme is based on an assumption known as "learning with errors" (LWE) - or, in more jargony but also more understandable terms, the hardness of solving systems of equations with errors.
A ciphertext can itself be viewed as an equation: \(k_1c_1 + .... + k_nc_n \approx 0\), where the key \(k_1 ... k_n\) is the unknowns, the ciphertext \(c_1 ... c_n\) is the coefficients, and the equality is only approximate because of both the message (0 or 1) and the error (\(2e\) for some relatively small \(e\)). The LWE assumption ensures that even if you have access to many of these ciphertexts, you cannot recover \(k\).
Note that in some descriptions of LWE, <c, k> can equal any value, but this value must be provided as part of the ciphertext. This is mathematically equivalent to the <c, k> = m+2e formulation, because you can just add this answer to the end of the ciphertext and add -1 to the end of the key, and get two vectors that when multiplied together just give m+2e. We'll use the formulation that requires <c, k> to be near-zero (ie. just m+2e) because it is simpler to work with.
Multiplying ciphertexts
It is easy to verify that the encryption is additive: if \(<ct_1, k> = 2e_1 + m_1\) and \(<ct_2, k> = 2e_2 + m_2\), then \(<ct_1 + ct_2, k> = 2(e_1 + e_2) + m_1 + m_2\) (the addition here is modulo \(p\)). What is harder is multiplication: unlike with numbers, there is no natural way to multiply two length-n vectors into another length-n vector. The best that we can do is the outer product: a vector containing the products of each possible pair where the first element comes from the first vector and the second element comes from the second vector. That is, \(a \otimes b = a_1b_1 + a_2b_1 + ... + a_nb_1 + a_1b_2 + ... + a_nb_2 + ... + a_nb_n\). We can "multiply ciphertexts" using the convenient mathematical identity \(<a \otimes b, c \otimes d> = <a, c> * <b, d>\).
Given two ciphertexts \(c_1\) and \(c_2\), we compute the outer product \(c_1 \otimes c_2\). If both \(c_1\) and \(c_2\) were encrypted with \(k\), then \(<c_1, k> = 2e_1 + m_1\) and \(<c_2, k> = 2e_2 + m_2\). The outer product \(c_1 \otimes c_2\) can be viewed as an encryption of \(m_1 * m_2\) under \(k \otimes k\); we can see this by looking what happens when we try to decrypt with \(k \otimes k\):
\[<c_1 \otimes c_2, k \otimes k>\] \[= <c_1, k> * <c_2, k>\] \[ = (2e_1 + m_1) * (2e_2 + m_2)\] \[ = 2(e_1m_2 + e_2m_1 + 2e_1e_2) + m_1m_2\]
So this outer-product approach works. But there is, as you may have already noticed, a catch: the size of the ciphertext, and the key, grows quadratically.
Relinearization
We solve this with a relinearization procedure. The holder of the private key \(k\) provides, as part of the public key, a "relinearization key", which you can think of as "noisy" encryptions of \(k \otimes k\) under \(k\). The idea is that we provide these encrypted pieces of \(k \otimes k\) to anyone performing the computations, allowing them to compute the equation \(<c_1 \otimes c_2, k \otimes k>\) to "decrypt" the ciphertext, but only in such a way that the output comes back encrypted under \(k\).
It's important to understand what we mean here by "noisy encryptions". Normally, this encryption scheme only allows encrypting \(m \in \{0,1\}\), and an "encryption of \(m\)" is a vector \(c\) such that \(<c, k> = m+2e\) for some small error \(e\). Here, we're "encrypting" arbitrary \(m \in \{0,1, 2....p-1\}\). Note that the error means that you can't fully recover \(m\) from \(c\); your answer will be off by some multiple of 2. However, it turns out that, for this specific use case, this is fine.
The relinearization key consists of a set of vectors which, when inner-producted (modulo \(p\)) with the key \(k\), give values of the form \(k_i * k_j * 2^d + 2e\) (mod \(p\)), one such vector for every possible triple \((i, j, d)\), where \(i\) and \(j\) are indices in the key and \(d\) is an exponent where \(2^d < p\) (note: if the key has length \(n\), there would be \(n^2 * log(p)\) values in the relinearization key; make sure you understand why before continuing).
Now, let us take a step back and look again at our goal. We have a ciphertext which, if decrypted with \(k \otimes k\), gives \(m_1 * m_2\). We want a ciphertext which, if decrypted with \(k\), gives \(m_1 * m_2\). We can do this with the relinearization key. Notice that the decryption equation \(<ct_1 \otimes ct_2, k \otimes k>\) is just a big sum of terms of the form \((ct_{1_i} * ct_{2_j}) * k_p * k_q\).
And what do we have in our relinearization key? A bunch of elements of the form \(2^d * k_p * k_q\), noisy-encrypted under \(k\), for every possible combination of \(p\) and \(q\)! Having all the powers of two in our relinearization key allows us to generate any \((ct_{1_i} * ct_{2_j}) * k_p * k_q\) by just adding up \(\le log(p)\) powers of two (eg. 13 = 8 + 4 + 1) together for each \((p, q)\) pair.
For example, if \(ct_1 = [1, 2]\) and \(ct_2 = [3, 4]\), then \(ct_1 \otimes ct_2 = [3, 4, 6, 8]\), and \(enc(<ct_1 \otimes ct_2, k \otimes k>) = enc(3k_1k_1 + 4k_1k_2 + 6k_2k_1 + 8k_2k_2)\) could be computed via:
\[enc(k_1 * k_1) + enc(k_1 * k_1 * 2) + enc(k_1 * k_2 * 4) + \]
\[enc(k_2 * k_1 * 2) + enc(k_2 * k_1 * 4) + enc(k_2 * k_2 * 8) \]
Note that each noisy-encryption in the relinearization key has some even error \(2e\), and the equation \(<ct_1 \otimes ct_2, k \otimes k>\) itself has some error: if \(<ct_1, k> = 2e_1 + m_1\) and \(<ct_2 + k> = 2e_2 + m_2\), then \(<ct_1 \otimes ct_2, k \otimes k> =\) \(<ct_1, k> * <ct_2 + k> =\) \(2(2e_1e_2 + e_1m_2 + e_2m_1) + m_1m_2\). But this total error is still (relatively) small (\(2e_1e_2 + e_1m_2 + e_2m_1\) plus \(n^2 * log(p)\) fixed-size errors from the realinearization key), and the error is even, and so the result of this calculation still gives a value which, when inner-producted with \(k\), gives \(m_1 * m_2 + 2e'\) for some "combined error" \(e'\).
The broader technique we used here is a common trick in homomorphic encryption: provide pieces of the key encrypted under the key itself (or a different key if you are pedantic about avoiding circular security assumptions), such that someone computing on the data can compute the decryption equation, but only in such a way that the output itself is still encrypted. It was used in bootstrapping above, and it's used here; it's best to make sure you mentally understand what's going on in both cases.
This new ciphertext has considerably more error in it: the \(n^2 * log(p)\) different errors from the portions of the relinearization key that we used, plus the \(2(2e_1e_2 + e_1m_2 + e_2m_1)\) from the original outer-product ciphertext. Hence, the new ciphertext still does have quadratically larger error than the original ciphertexts, and so we still haven't solved the problem that the error blows up too quickly. To solve this, we move on to another trick...
Modulus switching
Here, we need to understand an important algebraic fact. A ciphertext is a vector \(ct\), such that \(<ct, k> = m+2e\), where \(m \in \{0,1\}\). But we can also look at the ciphertext from a different "perspective": consider \(\frac{ct}{2}\) (modulo \(p\)). \(<\frac{ct}{2}, k> = \frac{m}{2} + e\), where \(\frac{m}{2} \in \{0,\frac{p+1}{2}\}\). Note that because (modulo \(p\)) \((\frac{p+1}{2})*2 = p+1 = 1\), division by 2 (modulo \(p\)) maps \(1\) to \(\frac{p+1}{2}\); this is a very convenient fact for us.
The scheme in this section uses both modular division (ie. multiplying by the modular multiplicative inverse) and regular "rounded down" integer division; make sure you understand how both work and how they are different from each other.
That is, the operation of dividing by 2 (modulo \(p\)) converts small even numbers into small numbers, and it converts 1 into \(\frac{p}{2}\) (rounded up). So if we look at \(\frac{ct}{2}\) (modulo \(p\)) instead of \(ct\), decryption involves computing \(<\frac{ct}{2}, k>\) and seeing if it's closer to \(0\) or \(\frac{p}{2}\). This "perspective" is much more robust to certain kinds of errors, where you know the error is small but can't guarantee that it's a multiple of 2.
Now, here is something we can do to a ciphertext.
Step 3 is the crucial one: it converts a ciphertext under modulus \(p\) into a ciphertext under modulus \(q\). The process just involves "scaling down" each element of \(ct'\) by multiplying by \(\frac{q}{p}\) and rounding down, eg. \(floor(56 * \frac{15}{103}) = floor(8.15533..) = 8\).
The idea is this: if \(<ct', k> = m*\frac{p}{2} + e\ (mod\ p)\), then we can interpret this as \(<ct', k> = p(z + \frac{m}{2}) + e\) for some integer \(z\). Therefore, \(<ct' * \frac{q}{p}, k> = q(z + \frac{m}{2}) + e*\frac{p}{q}\). Rounding adds error, but only a little bit (specifically, up to the size of the values in \(k\), and we can make the values in \(k\) small without sacrificing security). Therefore, we can say \(<ct' * \frac{q}{p}, k> = m*\frac{q}{2} + e' + e_2\ (mod\ q)\), where \(e' = e * \frac{q}{p}\), and \(e_2\) is a small error from rounding.
What have we accomplished? We turned a ciphertext with modulus \(p\) and error \(2e\) into a ciphertext with modulus \(q\) and error \(2(floor(e*\frac{p}{q}) + e_2)\), where the new error is smaller than the original error.
Let's go through the above with an example. Suppose:
\(<ct, k> = 5612 * 9 = 50508 = 9999 * 5 + 2 * 256 + 1\), so \(ct\) represents the bit 1, but the error is fairly large (\(e = 256\)).
Step 2: \(ct' = \frac{ct}{2} = 2806\) (remember this is modular division; if \(ct\) were instead \(5613\), then we would have \(\frac{ct}{2} = 7806\)). Checking: \(<ct', k> = 2806 * 9 = 25254 = 9999 * 2.5 + 256.5\)
Step 3: \(ct'' = floor(2806 * \frac{113}{9999}) = floor(31.7109...) = 31\). Checking: \(<ct'', k> = 279 = 113 * 2.5 - 3.5\)
Step 4: \(ct''' = 31 * 2 = 62\). Checking: \(<ct''', k> = 558 = 113 * 5 - 2 * 4 + 1\)
And so the bit \(1\) is preserved through the transformation. The crazy thing about this procedure is: none of it requires knowing \(k\). Now, an astute reader might notice: you reduced the absolute size of the error (from 256 to 2), but the relative size of the error remained unchanged, and even slightly increased: \(\frac{256}{9999} \approx 2.5\%\) but \(\frac{4}{113} \approx 3.5\%\). Given that it's the relative error that causes ciphertexts to break, what have we gained here?
The answer comes from what happens to error when you multiply ciphertexts. Suppose that we start with a ciphertext \(x\) with error 100, and modulus \(p = 10^{16} - 1\). We want to repeatedly square \(x\), to compute \((((x^2)^2)^2)^2 = x^{16}\). First, the "normal way":
The error blows up too quickly for the computation to be possible. Now, let's do a modulus reduction after every multiplication. We assume the modulus reduction is imperfect and increases error by a factor of 10, so a 1000x modulo reduction only reduces error from 10000 to 100 (and not to 10):
The key mathematical idea here is that the factor by which error increases in a multiplication depends on the absolute size of the error, and not its relative size, and so if we keep doing modulus reductions to keep the error small, each multiplication only increases the error by a constant factor. And so, with a \(d\) bit modulus (and hence \(\approx 2^d\) room for "error"), we can do \(O(d)\) multiplications! This is enough to bootstrap.
Another technique: matrices
Another technique (see Gentry, Sahai, Waters (2013)) for fully homomorphic encryption involves matrices: instead of representing a ciphertext as \(ct\) where \(<ct, k> = 2e + m\), a ciphertext is a matrix, where \(k * CT = k * m + e\) (\(k\), the key, is still a vector). The idea here is that \(k\) is a "secret near-eigenvector" - a secret vector which, if you multiply the matrix by it, returns something very close to either zero or the key itself.
The fact that addition works is easy: if \(k * CT_1 = m_1 * k + e_1\) and \(k * CT_2 = m_2 * k + e_2\), then \(k * (CT_1 + CT_2) = (m_1 + m_2) * k + (e_1 + e_2)\). The fact that multiplication works is also easy:
\(k * CT_1 * CT_2\) \(= (m_1 * k + e_1) * CT_2\) \(= m_1 * k * CT_2 + e_1 * CT_2\) \(= m_1 * m_2 * k + m_1 * e_2 + e_1 * CT_2\)
The first term is the "intended term"; the latter two terms are the "error". That said, notice that here error does blow up quadratically (see the \(e_1 * CT_2\) term; the size of the error increases by the size of each ciphertext element, and the ciphertext elements also square in size), and you do need some clever tricks for avoiding this. Basically, this involves turning ciphertexts into matrices containing their constituent bits before multiplying, to avoid multiplying by anything higher than 1; if you want to see how this works in detail I recommend looking at my code: https://github.com/vbuterin/research/blob/master/matrix_fhe/matrix_fhe.py#L121
In addition, the code there, and also https://github.com/vbuterin/research/blob/master/tensor_fhe/homomorphic_encryption.py#L186, provides simple examples of useful circuits that you can build out of these binary logical operations; the main example is for adding numbers that are represented as multiple bits, but one can also make circuits for comparison (\(<\), \(>\), \(=\)), multiplication, division, and many other operations.
Since 2012-13, when these algorithms were created, there have been many optimizations, but they all work on top of these basic frameworks. Often, polynomials are used instead of integers; this is called ring LWE. The major challenge is still efficiency: an operation involving a single bit involves multiplying entire matrices or performing an entire relinearization computation, a very high overhead. There are tricks that allow you to perform many bit operations in a single ciphertext operation, and this is actively being worked on and improved.
We are quickly getting to the point where many of the applications of homomorphic encryption in privacy-preserving computation are starting to become practical. Additionally, research in the more advanced applications of the lattice-based cryptography used in homomorphic encryption is rapidly progressing. So this is a space where some things can already be done today, but we can hopefully look forward to much more becoming possible over the next decade.